You simply need to know - Nanoscale
Nanoscale
Today’s magnetism research, materials with nanoscale dimensions and phenomena associated with surfaces, thin films, and interfaces are of prime importance. This has led to an increased demand for techniques with high sensitivity to small amounts of magnetic material or a small number of magnetic atoms. The atomic sensitivity of different techniques based on neutrons, electrons or X-rays may be expressed by a figure of merit per atom per second (FOM), defined by the product of the respective atomic interaction cross-section, the available incident flux, and the square of the magnetic contrast.
The new structures of interest have nanoscale sizes in at least one direction so that interfacial and surface properties often dominate their static magnetic structure and transport behavior.
The science and technology of magnetic materials is largely fuelled by the 50 billion dollars per year magnetic storage industry. Of interest are sandwiched magnetic sensors or “read heads”, such as spin valves, and magnetic“media” consisting of ferromagnetic thin films and multilayers that can store information in nanosized “bits”. On the horizon are nanoscale magnetic memory structures that are read out by their tunneling magnetoresistance which depends on the relative orientation of the magnetization in different layers.
Today’s magnetic materials are not the bulk materials of old, but atomically engineered thin film and multilayer structures that often have lateral dimensions on the nanometer scale. The study and understanding of such materials requires the use of better experimental and theoretical techniques that can give reliable information for the new low-dimensional materials.
In today’s devices magnetic switching times are about one nanosecond. In advanced recording studies times as short as 100 picoseconds have been achieved. The future of the magnetic storage and memory technology is dependent on new materials that are patterned or can self-assemble on the nanoscale and are magnetically stable at room temperature, on new materials and structures that at room temperature exhibit large magnetoresistance changes in small external fields, and on the development of methods to manipulate the magnetization on the subnanosecond time scale. An important challenge is the understanding of the size and speed limits of magnetic technologies.
Article src: Magnetism: From Fundamentals to Nanoscale Dynamics, J. Stohr, H.C. Siegmann, Springer-Verlag Berlin Heidelberg, 2006.
Magnetic moment
Magnetism in the solid state comprises a large variety of phenomena that can be characterized by quantities like the magnetic moment, the magnetic order, the ordering temperature, the magnetization direction, and so on. The physical concepts, used to describe these quantities on a theoretical basis, are again diverse and include relativistic quantum mechanics, statistical theories, and classical electrodynamics.
The magnetic moment of a solid can be obtained, for example, by quantum-mechanical theories, while ordering temperatures can be accessed by statistical theories which use input parameters of quantum-mechanical calculations. Exchange interactions have to be described on a quantum-mechanical basis, but it is usually sufficient to describe dipole–dipole interactions classically.
Although there is no single theoretical approach to all magnetic phenomena, it can be stated that magnetism is a uniquely quantum-mechanical phenomenon and, in the solid state, DFT is the most widespread theoretical method used to determine the magnetic properties of matter. Vector-spin density functional theory (DFT) allows – at least in principle – the access to the spin magnetic moment and the magnetic order of the ground state and it can serve to extract other quantities, like exchange interactions, that can serve as input for other theoretical approaches.
Article src: Handbook of Magnetism and Advanced Magnetic Materials, H. Kronmuller and S. Parkin, Volume 1: Fundamentals and Theory, John Wiley & Sons, 2007.
Magnetic dipole moment
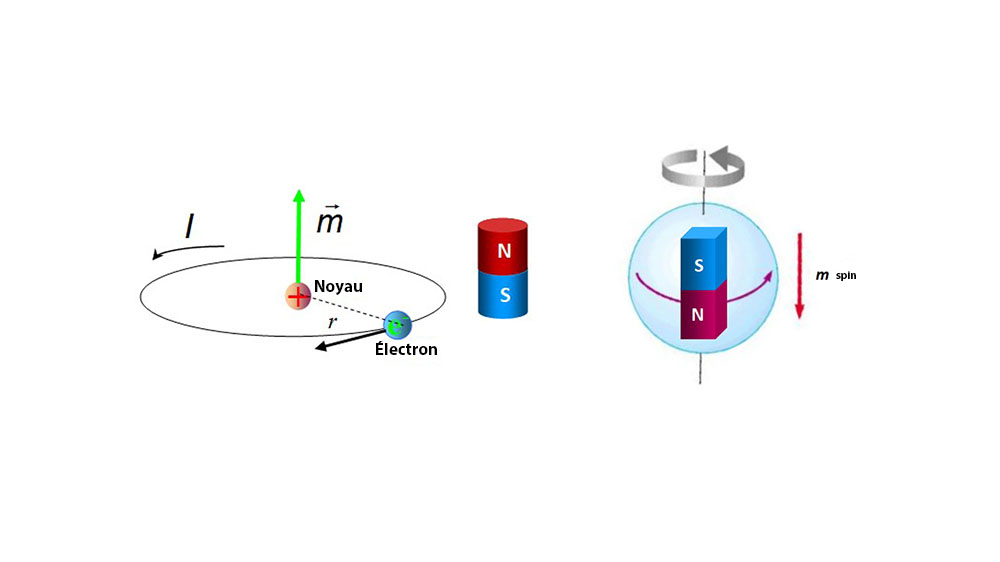
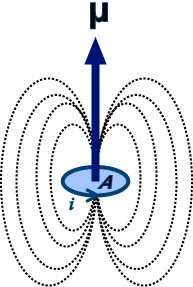
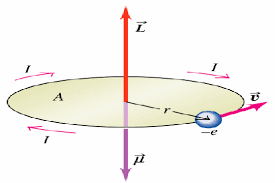
The elementary quantity in solid-state magnetism is the magnetic moment m. On an atomic scale, intrinsic magnetic moments are associated with the spin of each electron and a further contribution is associated with its orbital motion around the nucleus. The nucleus itself may possess spin, but the corresponding nuclear moments are three orders of magnitude smaller than those associated with electrons, because the magnetic moment of a particle scales as 1/mass. We can often neglect them.
The spin and orbital moments of the atomic electrons add in ways governed by the laws of quantum mechanics, discussed in the next two chapters. Suffice it to say that most of them manage to cancel out, and only a few transition metal atoms or ions retain a resultant moment on the atomic scale in solids. Again these atomic moments sum to zero in the paramagnetic state, unless an external magnetic field is applied, but for a different reason – they are disordered by thermal fluctuations. However, resultant moments do arise spontaneously within domains in the ferromagnetically ordered state.
Article src: Magnetism and Magnetic Materials, J. M. D Coey, Cambridge University Press, 2010.
Bohr magneton
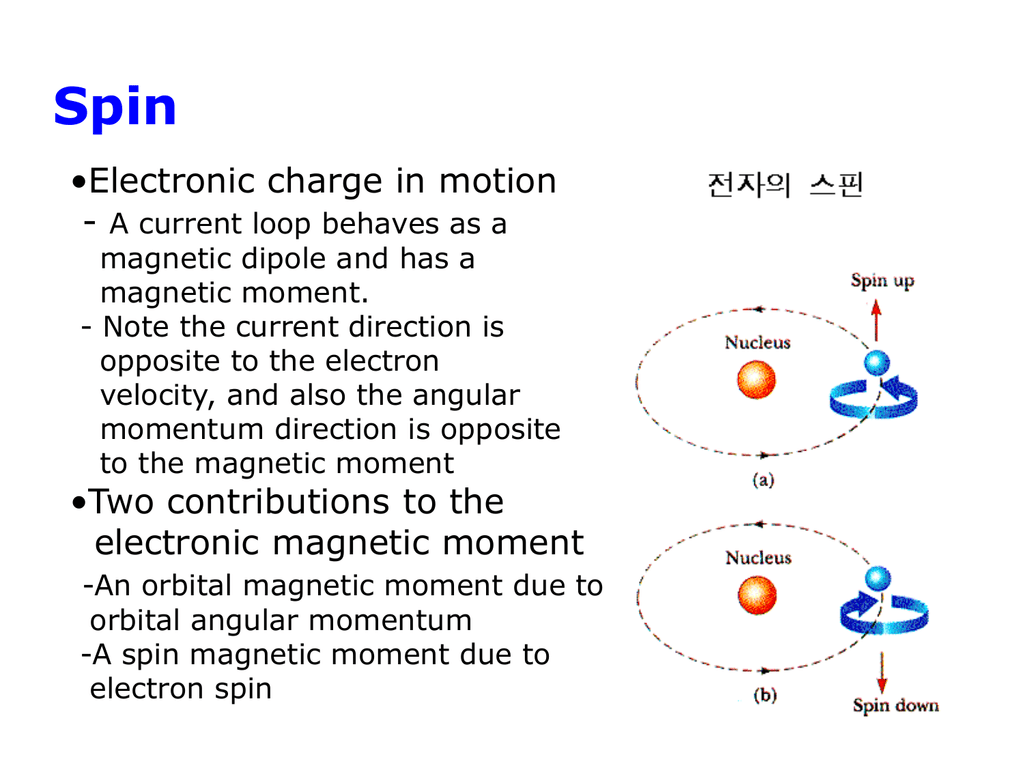
Strangely, the Amperian currents turned out to be associated with quantized angular momentum, and especially with the intrinsic spin of the electron, discovered by George Uhlenbeck and Samuel Goudsmit in 1925. The spin is quantized in such a way that it can have just two possible orientations in a magnetic field, ‘up’ and ‘down’. Spin is the source of the electron’s intrinsic magnetic moment, which is known as the Bohr magneton:
μB= 9.274 × 10−24 A m2.
The magnetic properties of solids arise essentially from the magnetic moments of their atomic electrons.
Thus the magnetic moment due to spin and that due to motion in the first Bohr orbit are exactly equal. Because it is such a fundamental quantity, this amount of magnetic moment is given a special symbol μB and a special name, the Bohr magneton. Thus,
μB = Bohr magneton = eh/4πmc = 0,927 x10-20 erg=Oe (cgs)
= eh/4πm = 9,27 x 10-24 A m2 (SI)
It is a natural unit of magnetic moment, just as the electronic charge e is a natural unit of electric charge.
How can the magnetic moment due to spin be understood physically? We may, if we like, imagine an electron as a sphere with its charge distributed over its surface. Rotation of this charge produces an array of tiny current loops, each of which has a magnetic moment directed along the rotation axis. But if we calculate the resultant moment of all these loops, we obtain the wrong answer, (5/6) μB instead of μB. Nor does the right answer result from the assumption that the charge is uniformly distributed through the volume of the sphere. Such calculations are fruitless, because we do not know the shape of the electron or the way in which charge is distributed on or in it. The spin of the electron, and its associated magnetic moment, has to be accepted as a fact, consistent with wave mechanics and with a large number of experiments of various kinds, but with no basis in classical physics.
Article src: Magnetism and Magnetic Materials, J. M. D Coey, Cambridge University Press, 2010.
Article src: Introduction to Magnetic Materials (2nd Edition), B. D. Cullity, C. D. Graham, Wiley-IEEE Press, 2008.
Magnetic moment of electrons
The magnetic moments in solids are associated with electrons. The microscopic theory of magnetism is based on the quantum mechanics of electronic angular momentum, which has two distinct sources – orbital motion and spin. They are coupled by the spin–orbit interaction. Free electrons follow cyclotron orbits in a magnetic field, whereas bound electrons undergo Larmor precession, which gives rise to orbital diamagnetism. The description of magnetism in solids is fundamentally different depending on whether the electrons are localized on ion cores, or delocalized in energy bands. A starting point for discussion of magnetism in metals is the free-electron model, which leads to temperature-independent Pauli paramagnetism and Landau diamagnetism. By contrast, localized noninteracting electrons exhibit Curie paramagnetism.
Moreover, in our world, electrons play a more important role than the positrons of the antiworld. The historical choices that the electron has a negative charge q = −e (we shall always assume that e = 1.602×10−19 C is a positive number) and the definition that the current I reflects the motion of positive charges is somewhat of a nuisance because the electrons move against the direction of the electric current. Another consequence of the negative charge of the electron is that the most important quantity of magnetism, the magnetic moment of the electron, is directed antiparallel to its intrinsic angular momentum, the spin. In this chapter we will define and discuss two basic quantities of magnetism, the static electric and magnetic fields.
The magnetization density and the magnetization, equation, are clearly a consequence of the imbalance of electrons with spin-up or spin-down and, therefore, the quantity defined in equation is called spin moment. From atomic physics we know that the total magnetic moment is a sum of spin and orbital contributions, Mtot = Mspin +Morb. The orbital moment results, in a classical picture, from the orbital motion of the electron around the nucleus. Compared to the situation in a free atom, where Morb can be even larger than Mspin, in a solid this motion is restricted by the crystal field that quenches the orbital moment. In bulk samples, small moments (typically 0.1–0.2μB) can be found.
Article src: Handbook of Magnetism and Advanced Magnetic Materials, H. Kronmuller and S. Parkin, Volume 1: Fundamentals and Theory, John Wiley & Sons, 2007.
Article src: Magnetism: From Fundamentals to Nanoscale Dynamics, J. Stohr, H.C. Siegmann, Springer-Verlag Berlin Heidelberg, 2006.
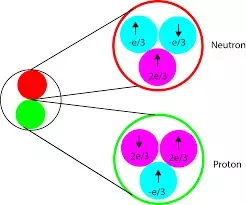
Magnetic moments of neutrons
Neutrons have a net magnetic moment of 5.4 x 10-4 Bohr magnetons (= 5.0 X 10- 27 Am2) but have no electric charge. This presence of magnetic moment in the absence of charge is itself an anomaly, but we shall not discuss the problem here. Nevertheless this combination of properties means that neutrons can pass relatively easily through a solid since they are not influenced by the localized electric charge distribution. The neutrons do interact with the nuclei to a greater or lesser extent depending on the type of nuclei. This gives rise to a nuclear scattering component in the total neutron diffraction spectrum. For the wavelengths used in neutron diffraction the nuclei act as point scatterers and the nuclear scattering spectrum is therefore isotropic.
The neutrons necessary for neutron diffraction studies of this type must have wavelengths comparable with the atomic dimensions, which are typically 0.1 nm. Neutrons with de Broglie wavelengths of this order of magnitude are produced in a nuclear reactor as thermal neutrons at a temperature of about 300 K and hence an energy of 4 x 10-21 J (25 meV) and a corresponding wavelength of 0.18 nm.
Article src: Introduction to Magnetism and Magnetic Materials (1nd edition), David Jiles, Chapman & Hall/CRC, 1991.
Angular momentum and its role in magnetism
Atoms contain many electrons, each spinning about its own axis and moving in its own orbit. The magnetic moment associated with each kind of motion is a vector quantity, parallel to the axis of spin and normal to the plane of the orbit, respectively. The magnetic moment of the atom is the vector sum of all its electronic moments, and two possibilities arise:
- The magnetic moments of all the electrons are so oriented that they cancel one another out, and the atom as a whole has no net magnetic moment. This condition leads to diamagnetism.
- The cancellation of electronic moments is only partial and the atom is left with a net magnetic moment. Such an atom is often referred to, for brevity, as a magnetic atom. Substances composed of atoms of this kind are para-, ferro-, antiferro-, or ferrimagnetic.
To calculate the vector sum of the magnetic moments of all the electrons in any particular atom is a rather complex problem which is treated in any book on atomic physics. However, this problem is not particularly relevant here because the result applies only to the free atom, such as the atoms in a monatomic gas. The calculation from first principles of the net magnetic moment of an atom in a solid is, in general, not yet possible, and the net moment must be determined experimentally. This knowledge of atomic moments, obtained experimentally, is of great importance in the continued development of solid-state physics, entirely aside from its relevance to commercially important magnetic materials.
Article src: Magnetism and Magnetic Materials, J. M. D Coey, Cambridge University Press, 2010.
Nuclear spins
It is not only the electrons in an atom which have a magnetic moment. The nucleus often has a non-zero spin resulting from the angular momentum of the nucleus. For each nucleus there is a quantum number, I, called the nuclear spin quantum number which represents the total angular momentum of the nucleus in units of h. However this magnetic moment is very small since its size scales with the inverse of the mass of the particles involved: nuclear moments are thus typically a thousand times smaller than electronic moments (most are between 10-3 and 10-4 μB). The small size and absence of any strong interaction between nuclei in adjacent atoms precludes the ordering of nuclear spin systems at ordinary laboratory temperatures.
Article src: Magnetism and Magnetic Materials, J. M. D Coey, Cambridge University Press, 2010.