Down to nanoscale - Effects
Changes in coercivity
Img src
One of the reported effects of dot interaction is the change in coercivity, which corresponds to the switching field discussed under the dipole context. Contradictory results have been reported in different materials (e.g., Co, Ni, Ni80Fe20), or for differently shaped elements or arrays of the same material (e.g., Ni80Fe20). Coercivity enhancement, reduction or insensitivity to dot separation can be found in the literature. For example, an increase of HC of 800 Oe has been reported for pairs of rectangular Co dots when the center-to center distance between dots has been decreased from 1 mm to 150 nm (with a corresponding 50nm gap between dot edges); while rectangular arrays of rectangular Ni80Fe20 dots exhibit a decrease of 100Oe in HC when reducing the center-to-center distance from about 1 mm to 200 nm (50nm gap); or no change in the collective coercivity has been observed in a linear array of rectangular Ni80Fe20 dots when reducing spacing from 2 mm to 250nm (50nm gap). Hence, these discrepancies are probably due to a number of factors, such as the type of array, magnetization state of the dots, switching mechanisms, and the fact that the nanodots are not simple dipoles. We have to stress that the field resulting from the dipolar interaction depends on the magnetization state of each dot, which in turn depends on the effective field of the neighboring elements. Consequently, the dipolar fields will change during the magnetization process. An example of the complex behavior due to interaction can be found in figure, where the switching mechanism appears to change (from rotation to vortex creation) as the dots are brought closer together with the resulting reduction in coercivity.
Article src: Ordered magnetic nanostructures: fabrication and properties, J.I. Martiın, J. Nogues, K. Liu, J.L. Vicent, I. K. Schuller, Journal of Magnetism and Magnetic Materials 256, 449-501, 2003.
Domain walls in nanowires
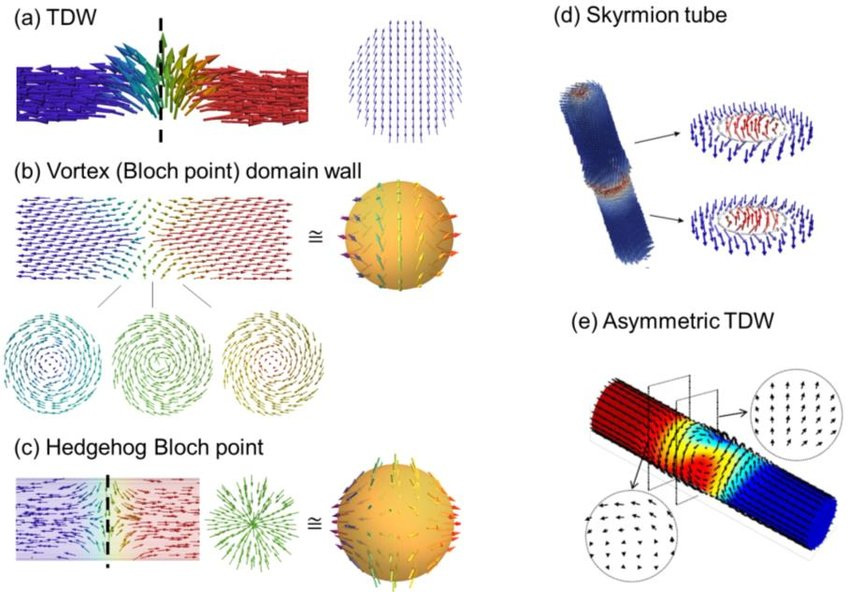
Img src
Magnetic Domain walls (DWs) have been studied in bulk samples and thin films for nearly a century. DWs have structures which range from the simplest Bloch wall, which can be described analytically by a one-dimensional model, to complex two and three-dimensional structures. The most common DW structures found in soft magnetic nanowires, are the so-called head-to-head (or tail-to-tail) DWs. Also, Bloch walls, which can be found in nanowires formed from materials with large perpendicular magnetic anisotropy.
Domain walls in soft magnetic nanowires
Macroscopic magnetic structures will typically form flux closed magnetic domain structures, which lower their energy. In sufficiently narrow nanowires made from soft magnetic materials, for example, submicron-wide permalloy (Ni81Fe19) wires, flux-closed domain structures are no longer energetically favored. Rather, owing to the nanowire’s magnetic shape anisotropy, magnetic domains are aligned along the nanowire’s length, with magnetizations pointing toward (or away) from each another. These domains are separated by head-to-head (or tail-to-tail) DWs.
Article src: Handbook of Magnetism and Advanced Magnetic Materials, H. Kronmuller and S. Parkin. Volume 1: Fundamentals and Theory, John Wiley & Sons, 2007.
Exchange coupling
Img src
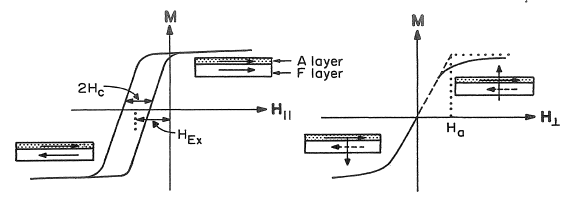
Exchange coupling refers to a preference for specific relative orientations of the moments of two different magnetic materials when they are in intimate contact with each other or are separated by a layer thin enough (< 60 Ả) to allow spin information to be communicated between the two materials. One material is generally magnetically softer and the other harder (or is antiferromagnetic).
Exchange coupling is manifest as a displacement of the loop of the soft material along its field axis. The term exchange coupling does not apply to dipole coupling, namely, the longer-range mutual influence of the magnetic moments of two nearby materials due to their dipole fields. Such magnetostatic coupling can arise from interfacial charges due to roughness of the boundary between two materials.
The ferromagnetic-antiferromagnetic (F/A) form of exchange coupling is considered first. In 1956 Meiklejohn and Bean observed that the M-H loops of fine cobalt particles (2r = 20 nm) could be displaced on the field axis by more than 1 kOe if the particles were cooled in a magnetic field.
Exchange coupling between dissimilar magnetic particles or layers, in contact or separated by a suitable spacer layer of a few nanometers, can give rise to new phenomena. Nonmagnetic nanostructured materials appear to have no mechanisms analogous to exchange coupling, except perhaps their long-range stress fields, that introduces a new characteristic length scale to material properties. The presence of the magnetic exchange interaction renders nanostructured magnetic materials versatile compared to less complex magnetic materials and distinguishes them from nonmagnetic nanostructured materials.
Article src: MODERN MAGNETIC MATERIALS: Principles and Applications, R. C. O' HANDLEY, Massachusetts Institute of Technology, John Wiley & Sons, 2000.
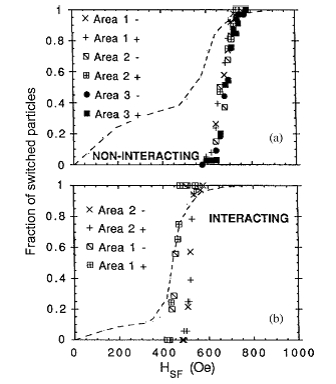
Interaction in arrays of dots
Img src
Due to the 1/r3 dependence of the dipole–dipole interaction, the effects of the interactions between dots depend strongly not only on the distance between the centers of the dots but also the distance between edges of the dots. Moreover, the effects of interaction, e.g. changes in the coercivity, will be more significant in systems with a small crystalline and shape anisotropy, i.e., with small saturation and coercive fields. In other words, it is easier to observe an effect of a 20 Oe interaction field in a system with a coercivity of 100 Oe than in one of 3000 Oe. Another important factor influencing the interaction among dots is the magnetization state of the dots. Usually the dots are assumed to be single domains, so they can be approximated by dipoles. However, often the dots are in magnetization states with reduced or no external flux at remanence (e.g., closure domains or vortex state). Such systems should have negligible interactions at fields close to H = 0 due to the m~0 state and the corresponding lack of stray fields.
Nevertheless, interactions could become significant as the external field is increased, resulting in nonzero dipolar moments; and they are often important for large applied fields when the dots become saturated.
Article src: Ordered magnetic nanostructures: fabrication and properties, J.I. Martiın, J. Nogues, K. Liu, J.L. Vicent, I. K. Schuller, Journal of Magnetism and Magnetic Materials 256, 449-501, 2003.
Magneto-optical properties of layered systems.
Img src
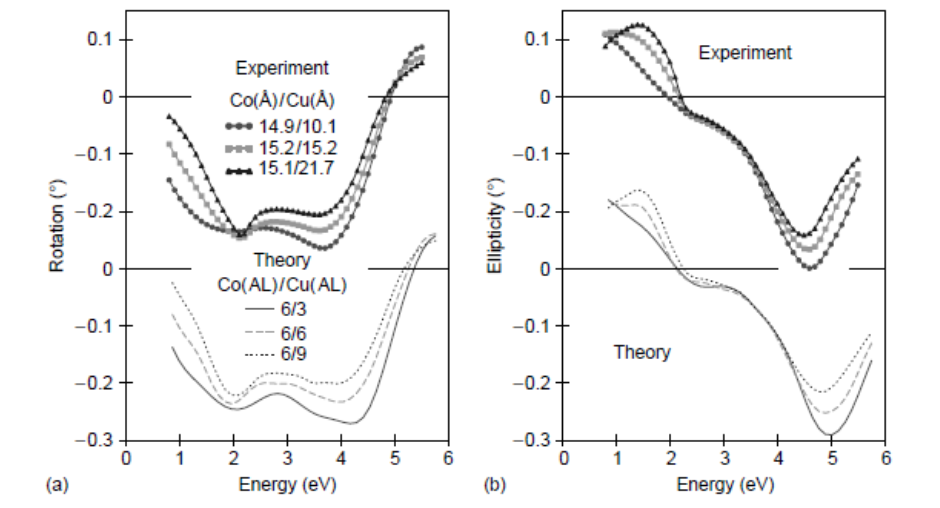
Most of the experimental as well as theoretical studies on the magneto-optical properties of transition metal systems were motivated by their application in sensor and storage technology. This applies in particular for the investigations on multilayers. These systems allow to some extent the optimization of Kerr rotation spectra with regard to the position and height of prominent peaks by a suitable combination of atomic layers and choice of their thickness. This is demonstrated in figure, which shows Kerr rotation and ellipticity spectra for the multilayer system 6Co/mCu with the thickness m of the Co layers varied between 3 and 9 atomic layers. The peak positions in the theoretical spectra are somewhat shifted as compared to the experimental ones because the local-field and correlation effects are neglected. The various features of the Kerr rotation and ellipticity spectra and their variation with the thickness of the Cu layers, however, are well described by the calculations. This implies, in particular, that imperfections at the Co/Cu interface have only a minor influence on the experimental spectra.
Extensive studies have also been made on the multilayer systems nCo/mPd and nCo/mPt because here the ferromagnetic component Co is combined with an element having a stronger spin-orbit coupling. In addition, Pd and Pt show a pronounced polarizability leading to an induced spin magnetic moment in the order of 0.2 μB at the interface. Furthermore, the high spin orbit coupling of Pd and Pt is one of the main reasons for the pronounced out-of-plane magnetic anisotropy of these Co-based multilayer systems.
Figure suggests that the calculation of the magnetooptical spectra of multilayer systems should lead, in general, to rather reliable results. On the other hand, it is obviously quite hard or impossible to explain the various spectral features and their variation with the multilayer composition on the basis of such calculations.
Article src: Handbook of Magnetism and Advanced Magnetic Materials, H. Kronmuller and S. Parkin. Volume 1: Fundamentals and Theory, John Wiley & Sons, 2007.
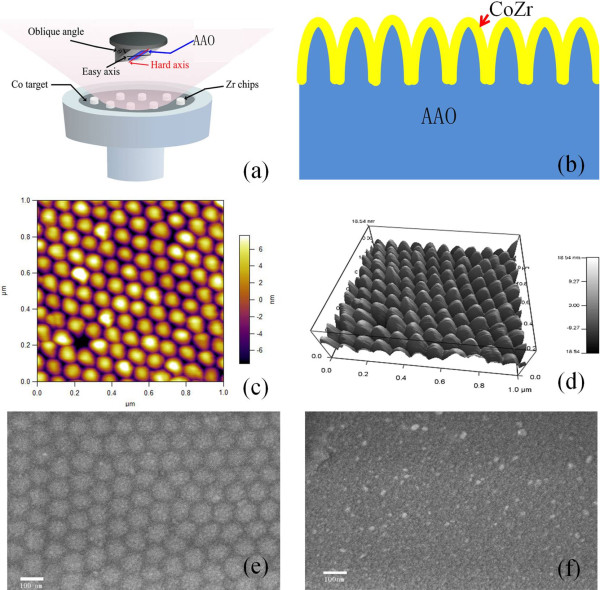
Nanowires

Img src
Shape control of nanoparticles such as nanowires and nanotubes provides an opportunity to tune shape anisotropy. Progress in experimental techniques has made it possible to synthesize nanowires with high aspect ratio. Among the methods used for fabrication of nanowire arrays, template-assisted electrodeposition is a low-cost and high-yield technique, and FePt nanowire preparation by electrodeposition and solvothermal synthesis has been reported; due to the high reduction potential of Nd, however, it is difficult to synthesize Nd2Fe14B nanowires by electrodeposition. In the solvothermal synthesis process, by controlling the surfactant concentration, different shapes and sizes of FePt nanoparticles can be synthesized. Due to the high anisotropy of nanowires, high coercivity of FePt nanowires is expected.
However, the coercivity observed is much smaller than the anisotropy field, suggesting that magnetization rotation is not coherent but involves domain nucleation and domain wall motion. The coercivity/magnetization reversal mechanism of nanowires is different from that of the bulk. The easy magnetization direction of nanowires is along the nanowire axes, and the overall magnetic anisotropy is dominated by the shape anisotropy.
Hysteresis loops exhibit greater squareness for fields applied parallel to the nanowire arrays compared with when the applied field is perpendicular. However, Cagon et al. observed no significant difference between curves with the field applied parallel or perpendicular to the wires. The magnetization reversal and coercivity of the nanowires are sensitive to the nanowire diameter. Magnetization reversal may occur by coherent rotation, magnetization curling, and buckling.
Article src: Handbook of Nanomaterials, Robert Vajtai, Springer-Verlag Berlin Heidelberg 2013.
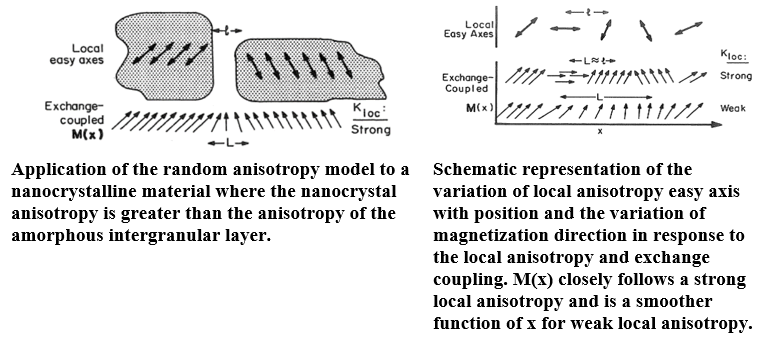
Random anisotropy
The concept of random anisotropy in continuous magnetic systems such as amorphous alloys was reviewed. It is illustrated how interparticle exchange and random anisotropy combine to affect the magnetic properties of discrete magnetic systems such as nanocrystalline alloys. In the random anisotropy situation, the effective anisotropy is reduced by averaging K1oc over the exchange length of the magnetic moments. In nanocrystalline materials, K1oc applies over the entire nanocrystal volume, and hence the appropriate length scale for the random anisotropy variation is given by the thickness of the interparticle layer. The variation in magnetization direction occurs over the intergranular material between the particle surfaces if K1oc is strong compared to the anisotropy of the intergranular, amorphous matrix Kam, or over a larger length if K1oc is comparable to K1oc.
Random anisotropy can promote spatial dispersion of the local moments, and the additional presence of more than one magnetic species can lead to a rich variety of magnetic structures with dispersed parallel (speromagnetic) or dispersed antiparallel [sperimagnetic (SM)] magnetic sublattices.
Alben et al. (1978) treat several fundamentals sues in amorphous ferromagnetism, notably the effects of random anisotropy on coercivity, spin wave demagnetization, and chemical versus structural disorder effects on the temperature dependence of magnetization.
However, the local atomic order of amorphous magnetic alloys, which varies randomly in direction, gives rise to a random anisotropy that plays an important role in their magnetic properties.
Magnetic anisotropy arising from long-range crystallinity is clearly absent in amorphous alloys. However, the same "crystal field" or more accurately "local-field that gives rise to magnetocrystalline anisotropy is effective in noncrystalline materials on a scale of a few nanometers. The orientation and strength of this local anisotropy in amorphous alloys varies with position, hence the term random anisotropy. It is important to determine the degree to which this random local anisotropy field affects macroscopic magnetic behavior or, on the other hand, is averaged out because of fluctuations in orientation of the local "easy axes".
The local crystal field energy can be represented by a uniaxial (dipolar) term of strength Kloc. The orientation of the easy direction of this uniaxial anisotropy in an amorphous alloy fluctuates with a correlation length I determined by the local structure: 1 is a few nanometers for amorphous alloys.
The concept of random anisotropy is also relevant in treating the variation in direction of magnetization from particle to particle. Another effect observed only in samples with at least one small dimension is the coupling between spins on different sides of a physical interface (exchange coupling). This phenomenon is critical to understanding the magnetic behavior of nanocrystalline materials and the behavior of many thin-film magnetic structures and devices. There are also transport effects in which the direction of spin in one magnetic layer is communicated across an interface by a current carrier to produce a spin-dependent scattering in another magnetic layer. In particular, when exchange coupling operates in the presence of a random anisotropy the technical magnetic properties, limited by the exchange-averaged anisotropy <K>, depend on the length scale of the random anisotropy to the sixth power.
Article src: MODERN MAGNETIC MATERIALS: Principles and Applications, R. C. O' HANDLEY, Massachusetts Institute of Technology, John Wiley & Sons, 2000.
Shape anisotropy

Img src
Shape anisotropy reaches a more critical role in nanostructures, since it is one of the most important aspects determining the magnetic state of the nanostructures, especially for polycrystalline systems and systems with small magnetic anisotropy.
In these cases, the shape anisotropy becomes much larger than the intrinsic anisotropies and can therefore dominate the magnetic behavior of the system. For example, polycrystalline rectangular or elliptical dots tend to have the easy axis along the long axis of the elements, or columnar dots along their length.
Surface anisotropy which becomes pronounced in dots where the surface-to-volume ratio is high. The reduction in coordination numbers of the surface atoms can introduce frustration and spin disorder. Even antiferromagnetic nanodots could develop net magnetizations at very small sizes. The configurational anisotropy is related to the small deviations of the spins from the parallel state at the corners of non-ellipsoidal dots, due to the non-homogeneous demagnetizing field.
Article src: Ordered magnetic nanostructures: fabrication and properties, J.I. Martiın, J. Nogues, K. Liu, J.L. Vicent, I. K. Schuller, Journal of Magnetism and Magnetic Materials, 256, 449-501, 2003.
Superparamagnetism
Img src
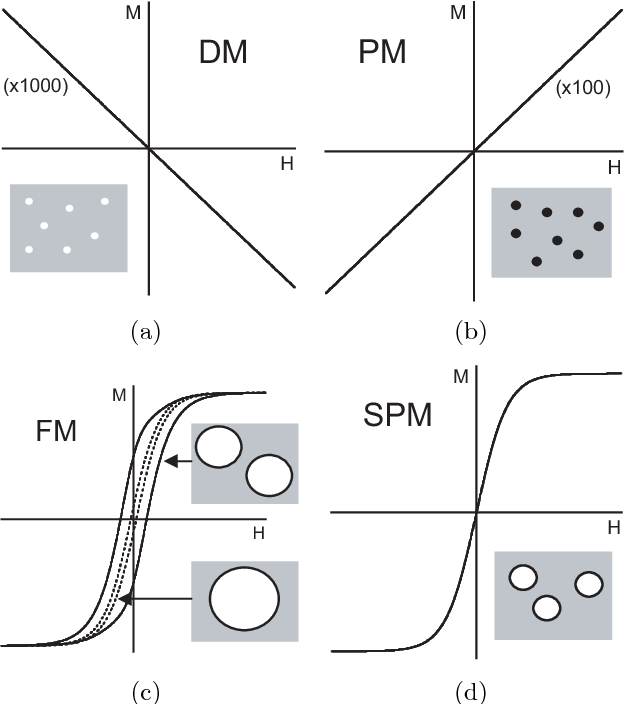
The existence of domains in magnetic materials leads to a hysteresis of the magnetization when it is measured as a function of increasing and decreasing applied DC magnetic field. When the size of an individual magnetic particle is reduced below some critical value, it is no longer energetically favorable to form domains and the particles have a single domain. For example, Fe2O3 nanoparticles become single domain below about 100 nm, and CoFe2O4 magnetic nanoparticles are single domain below 50 nm. The existence of single‐domain nanoparticles results in the phenomenon of superparamagnetism where the magnetization as a function of increasing and decreasing magnetic field displays no hysteresis.
Information storage density will be limited by physical factors such as superparamagnetism (zero coercivity implies loss of memory) in small storage elements and by magnetic resonance limitations at high read and write rates.
Superparamagnetism becomes a problem for particles smaller than about 10nm in diameter, corresponding to areal densities of about 20 Gb/in2.
Article src: Physics of Magnetic Nanostructures, First Edition. Frank J. Owens, Inc. Published by John Wiley & Sons, Inc., 2015.
Article src: MODERN MAGNETIC MATERIALS: Principles and Applications, ROBERT C. O' HANDLEY, Massachusetts Institute of Technology, John Wiley Pr Sons, 2000.
Thin-film
Thin-film or multilayer magnetic nanostructures have only one dimension in the nanoscale range. Magnetic and nonmagnetic layers are stacked to make heterostructured thin films, which have applications in spin valves, tunnel junctions, GMR, etc. Magnetic thin films show interesting magnetic phenomena such as perpendicular anisotropy, moment modifications at surfaces and interfaces, and thickness-dependent domain wall motion.
For thin films with perpendicular magnetic anisotropy, the saturation magnetization in the perpendicular direction is higher than that in the parallel direction. The perpendicular magnetic anisotropy in thin films is thickness dependent and vanishes with increasing film thickness, due to multidomain particle formation at larger thickness. At low thickness, Nd-Fe-B films are single domain and magnetization reversal is dominated by coherent rotation of magnetic domains, resulting in high coercivity. However, for larger thickness, the magnetization/demagnetization mechanism is different (domain wall motion) and results in low coercivity.
Article src: Handbook of Nanomaterials, R. Vajtai, Springer-Verlag Berlin Heidelberg, 2013.