You simply need to know - Microscale
Theory of micromagnetismm
The continuum theory of micromagnetism, which was developed in the 1930s and 1940s, was intended to bridge the gap between the phenomenological Maxwell’s theory of electromagnetic fields and quantum theory based on atomic backgrounds. In Maxwell’ s theory material properties are described by global permeabilities and susceptibilities valid for macroscopic dimensions. On the other hand quantum theory allows a description of magnetic properties on the atomistic level. Both theories are not suitable to describe cooperative and interactive phenomena such as macroscopic magnetization processes or hysteresis loops of ordered spin structures. The requirement to bridge the gap between Maxwell’s theory and quantum theory became very urgent after Barkhausen’s experiment known as Barkhausen’s jumps and Sixtus’ and Tonks’ experiment on the domain wall velocity.
A further landmark that proved the existence of the socalled Weiss domains was the Bitter experiment, where by using the dipolar interactions between magnetic ferrofluids and the magnetic stray fields exerting from domain walls the domain patterns were clearly visible.
After the explanation of ferromagnetism by Heisenberg (1928) and Dirac (1928) on the basis of exchange interactions, the door was wide opened toward a mesoscopic theory of magnetism combining Maxwell’s and quantum theory. A first attempt to treat inhomogeneous magnetic states is due to Bloch (1932) who showed that as a consequence of exchange interactions the transition regions between the Weiss domains have a finite width. Actually Bloch considered a type of domain wall, today called Neel wall; however, Bloch neglects the dipolar stray field energy, thus obtaining the result of the stray field free domain wall, now called the Bloch wall. The different type of domain walls have been outlined later by Neel, who gave a first approximate calculation of the so-called Neel wall.
The breakthrough toward a continuum theory of magnetism is due to Landau and Lifshitz (1935), who derived a continuum expression for the exchange energy and gave a first interpretation of domain patterns. In this context, the work by Akulov (1928–1931) should be mentioned, who derived continuum expressions for the magnetocrystalline energy. Here for the first time the interaction between magnetization and the microstructure has been considered by the derivation of the so-called magnetoelastic coupling energy for cubic crystals. It was the progress made in the 1930s with respect to microstructures, for example, the definition of dislocations as the sources of internal strains, which inspired W. F. Brown to publish in 1940 and 1941 two basic papers from which the modern theory of micromagnetism emerged. Brown in these papers for the first time considered the effect of local perturbations of the direction of magnetization on the law of approach to ferromagnetic saturation in order to find an explanation for the 1/H term usually found experimentally. There were further papers by Kittel, Stoner–Wohlfarth, Neel, Aharoni, Strikman, Treves and of course also Brown in the 1950s, who established the theory of micromagnetism as an efficient tool to describe magnetization processes and the characteristic properties of the hysteresis loop.
Whereas in the second half of the twentieth century micromagnetism was applied mainly to the classical problems of ferromagnetic materials in the twenty-first century the problems of magnetoelectronics and spintronics became relevant. Here the recent developments in computational micromagnetism play an important role. These techniques allow solutions of the nonlinear micromagnetic equations, determination of spin distribution of magnetic ground states, the determination of single-domain configurations and vortex states as well as the investigation of the dynamics of magnetization processes.
Article src: Handbook of Magnetism and Advanced Magnetic Materials, H. Kronmuller and S. Parkin, Volume 1: Fundamentals and Theory, John Wiley & Sons, 2007.
Domain theory
The magnetic domain, in theory and experiment, has had a curious history. Of the two great concepts introduced by Weiss in 1906, the domain hypothesis and the molecular field, Weiss himself stressed only the latter. Later investigators added very little. For a period of 43 years they made virtually no application of the domain idea to the problems of explaining the shape of a magnetization curve or the mechanism of magnetic hysteresis. During this period some isolated, though important, theoretical work was done, but the domain hypothesis was not brought into the mainstream of research on magnetic materials. Not until 1949 was there any direct experimental evidence for, and clear understanding of, the domain structure of a real material; in that year H. J. Williams, R. M. Bozorth, and W. Shockley published their work, performed at the Bell Telephone Laboratories, on domains in silicon-iron single crystals. Since that time, domain theory has become central to any discussion of magnetization processes.
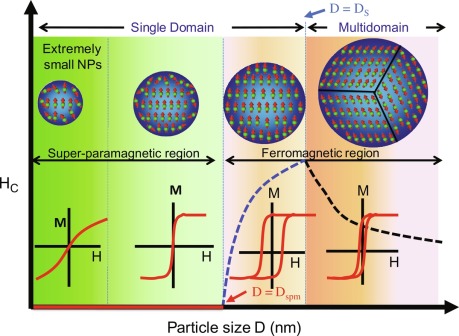
A remarkable property of ferrimagnetic materials is not so much that they have a spontaneous magnetization, but rather that their magnetization can be influenced by the application of very low magnetic fields. Even the earth's field (50 μT) can cause magnetization changes even though the interatomic exchange forces responsible for the spontaneous magnetization are equivalent to a field of about 1000 T, almost 100 million times greater than the earth's field. What allows this to occur is the fact that the sample is actually composed of small regions called magnetic domains, within each of which the local magnetization is saturated but not necessarily parallel. Domains are small (1-100's microns), but much larger than atomic distances.
Domains constitute a fundamental concept in magnetism. A ferro- or ferrimagnetic material may be generally defined as one that possesses a spontaneous magnetization, Ms, dependent on temperature, but only slightly dependent on applied field. The theory of ferromagnetism, based on electronic exchange forces, predicts the magnitude of Ms, but says nothing about the direction of Ms. Experimentally, it is observed that for a homogeneous specimen at constant temperature, the magnitude of Ms is uniform but the direction of Ms is in general not uniform from one region to another (on a scale of microns to millimeters). Uniformity of direction is attained only by applying a large enough field to drive the domains out of the sample, or by reducing the particle's dimensions to small enough size to prevent domain formation.
Article src: Introduction to Magnetic Materials (2nd Edition), B. D. Cullity, C. D. Graham, Wiley-IEEE Press, 2008.
Domain walls
The local magnetic properties in the vicinity of domain boundaries are regions which are called domain walls. They have properties which are very different from the rest of the domain. Most of the magnetic changes under the action of weak and moderate magnetic fields occur at the domain walls and hence an understanding of domain-wall behaviour is essential to describing the magnetizing process.
How do the magnetic moments behave in the domain boundaries?
Once we have accepted the idea of domains within ferromagnets there arises the question of how the moments change direction in the vicinity of the domain boundary. There are two possibilities, either the domain boundary is infinitesimal in width with nearest-neighbour moments belonging either to one domain or the other. Alternatively there could be a transition region in which the magnetic moments realign between the domains and therefore belong to neither domain.
How thick are the domain walls?
The existence of these transition layers between domains, in which the magnetic moments undergo a reorientation, was first suggested by Bloch. The transition layers are commonly referred to as domain walls or Bloch walls, although we should note immediately that not all domain walls are necessarily Bloch walls. The total angular displacement across a domain wall is often 180° or 90°, particularly in cubic materials because of the anisotropy and, as we shall see, the change in direction of the moments takes place gradually over many atomic planes.
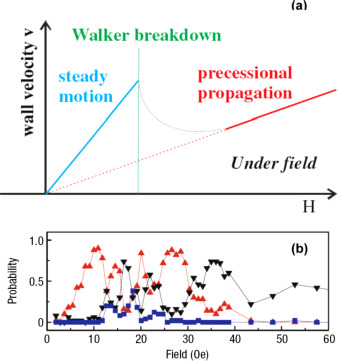
Magnetic domain walls occur in all forms of ordered magnetic materials and so there are correspondingly many different forms of domain walls. Domain walls in simple antiferromagnets and ferrimagnets are similar to domain walls in ferromagnets. However the helical antiferromagnet such as occurs in dysprosium and terbium presents a very interesting case. Domains in these materials were first suggested by Palmer in which it was suggested that the domains consisted of helices of different chirality. These were subsequently observed experimentally. The domain walls are transition regions between helical domains and are regions in which the neighbouring moments are aligned nearly parallel, or at least the turn angle between successive moments ¢ is very small compared to within the domain. Generally the two senses of helix are energetically equal so that either may occur. Application of a field perpendicular to the unique axis of the helix can cause favourably oriented domain walls to grow. Therefore the helical to ferromagnetic transition, which can be induced by application of a field perpendicular to the unique axis, is caused by growth of domain walls in this type of magnet.
Article src: Introduction to Magnetism and Magnetic Materials (1nd edition), David Jiles, Chapman & Hall/CRC, 1991.
Weiss domains
It is a common experience that pieces of ferromagnetic material do not always exhibit a north pole and a south pole. They often appear to be demagnetized or even nonmagnetic in the presence of another soft magnetic body. Only when placed in an external field or near a permanent magnet do soft magnetic materials begin to respond and reveal their magnetism. The demagnetization of soft magnetic materials was attributed by Weiss to the formation of magnetic domains that are regions inside the material that are magnetized in different directions so that the net magnetization is nearly zero. Before questions about the arrangement and size sf magnetic domains can be addressed, it is important to understand the spin structure and energy density of the surfaces, called domain walls, that separate one domain from another. Then, the energy of different domain wall arrangements in a material will bebalanced against the magnetostatic energy cost of having a single domain.
But how is iron magnetized or demagnetized? Weiss came up with an hypothesis for that, too. He postulated the existence of magnetic domains, regions (ranging in size upwards from approximately 0.1 pm) in a ferromagnetic material over which all moments are essentially parallel. Domains are separated from each other by domain walls.
Article src: Modern magnetic materials : principles and applications, Robert C. O' Handley, John Wiley Pr Sons, 2000.
Domain-wall pinning
The inclusion theory of domain-wall pinning was suggested by Kersten. He assumed that the magnetic domain walls move in a planar manner through the solid and that the energy of the walls is reduced when they intersect inclusions. The inclusions themselves may take many forms such as insoluble second-phase material which appears if the solubility limit has been exceeded, they may be oxides or carbides, or they may be pores, voids, cracks or other mechanical inhomogeneities. Well-known examples of magnetic inclusions are cementite (Fe3C) particles in iron and steels.
Can realistic models of the magnetization process be devised from the concept of domain-wall pinning?
One of the most difficult problems in the field of magnetism is to describe the magnetization curves of a ferromagnet in terms of materials properties. The complexity of domain-wall interactions with randomly distributed structural features is further compounded by the possibility of magnetization changes by domain rotation. Therefore attempts at deriving the underlying theory have dealt only with the simplest situations.
We will become more familiar with an interesting phenomenon known as magnetic Barkhausen noise which is based on magnetic microstructures, in particular, domain wall pinning by obstacles. Some technological applications of the thin film type exploit magnetic domains, or thickness-dependent domain wall and coercive phenomena. Many magnetic nondestructive evaluation techniques exploit other specific micromagnetic properties to detect flaws and strains on the surface of engineering components. On the other hand, traditional magnetic tapes for information storage still struggle with energetic losses created in the material because of their microstructure, and need to minimize these losses.
Article src: Handbook of modern ferromagnetic materials, A. Goldman, B.S., Springer Science+Business Media New York, Ferrite Technology Worldwide, (1st edition), 1999.
Article src: Introduction to Magnetism and Magnetic Materials (1nd edition), David Jiles, Chapman & Hall/CRC, 1991.
Nucleation of reversed domains
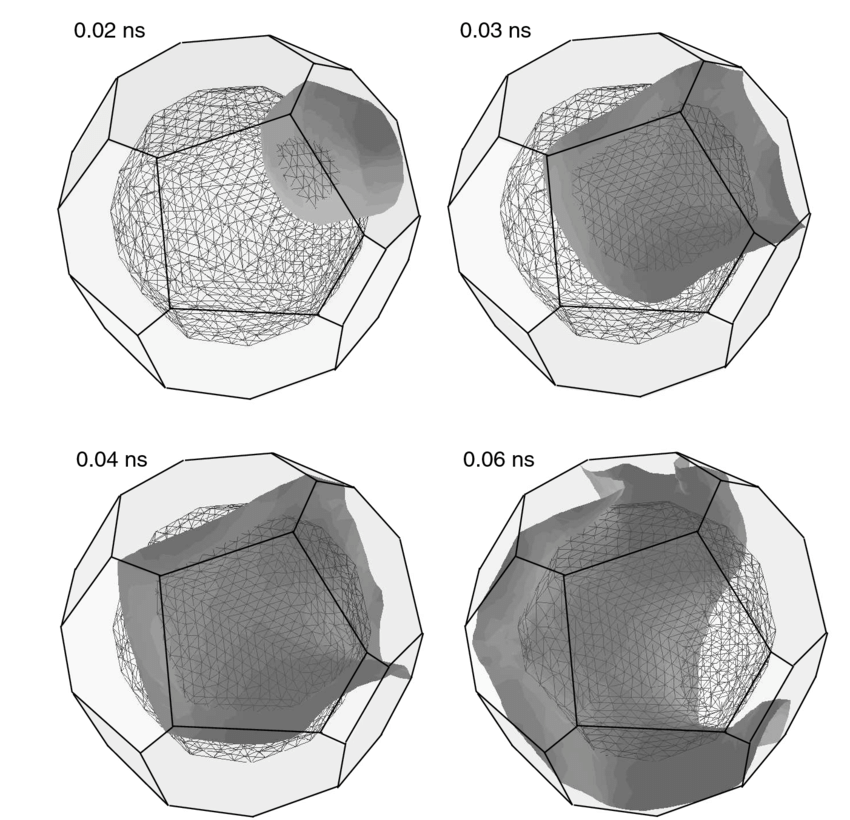
The large coercive fields of permanent magnets and, therefore, the magnetic hardening are alternatively accomplished by two basic mechanisms – reversal of the magnetization by nucleation of reversed domains (nucleation mechanism) or reversal of the magnetization by displacement of pinned domain walls (pinning mechanism). For both hardening mechanisms the coercivity can be well described in the framework of the theory of micromagnetism by the universal relation.
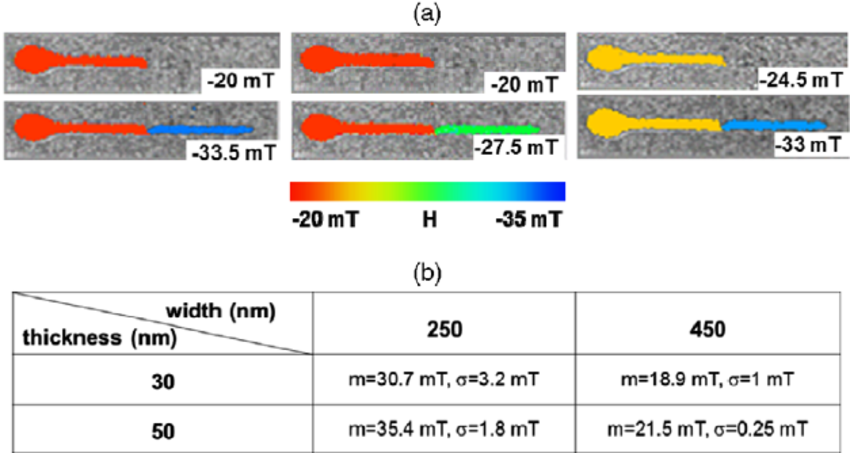
However, for the rougher films the domains show a high degree of correlation during the nucleation, and the correlation becomes reduced further along during the magnetization reversal. This indicates that if there are enough defects present in the magnetic system the nucleation of reversed domains occurs at identical defects, but the motion of domain walls is more random thereafter.
The nucleation of reversed domains takes place in regions with low magnetocrystalline anisotropy. RE-rich precipitates mainly deteriorate the JHc of the final magnet. The reason for the formation of these phases is due to the addition of a RE-rich sintering aid phase before the sintering process. The coercivity can be improved by adding small amounts of TM powders or TM oxides. Transmission electron micrographic (TEM) studies shows that the chemical composition, the size distribution and the impurity content (oxygen content) of the starting powder material are important factors for the magnetic properties of SmCo5-type sintered magnets.
Article src: Handbook of Magnetism and Advanced Magnetic Materials, H. Kronmuller and S. Parkin, Volume 1: Fundamentals and Theory, John Wiley & Sons, 2007.
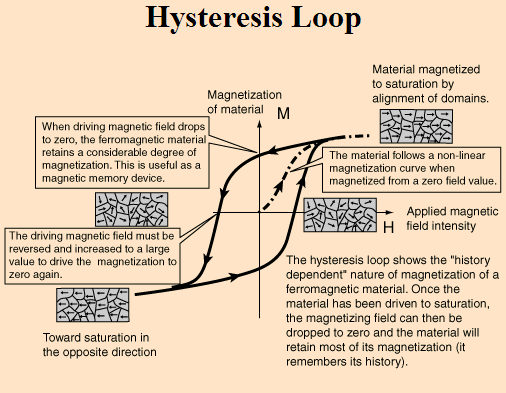
Hysteresis loop
In bulk material, it is practically impossible to calculate a complete hysteresis loop precisely.
Hard magnetic materials whose magnetization process is governed by nucleation or pinning are readily distinguished by their initial magnetization curves. The domain walls move freely through a nucleation-type magnet, which has a high initial susceptibility, but they are constantly being trapped in a pinning type magnet, so the initial susceptibility is small until the depinning field is reached. Coherent rotation, the dominant reversal mechanism in a uniaxial system, is provided by the dependence of coercivity on the angle between the applied field and the easy axis. This varies as cos α in the Stoner– Wohlfarth model, whereas if nucleation is involved, it is only the component of field along the easy axis which is effective at creating reversal, hence there is a 1/ cosa dependence.
In soft magnetic materials, the hysteresis in the initial region in fields which are small compared with the saturation coercivity is described by the empirical Raleigh laws enunciated by John Strutt in 1887.
Article src: Magnetism and Magnetic Materials, J. M. D Coey, Cambridge University Press, 2010.